Research Projects

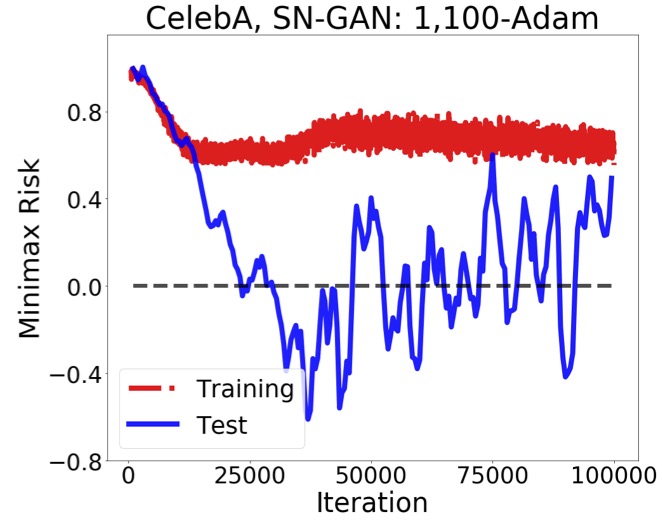Abstract: The success of minimax learning frameworks has been empirically observed to depend on the optimization algorithm used for their training. In this work, we present theoretical and numerical evidence showing that the generalization properties of learned minimax models are influenced by the underlying optimization algorithm. To this end, we extend the classical algorithmic stability approach to gradient-based minimax optimization algorithms and analyze the generalization properties of standard gradient descent ascent and proximal point method algorithms. Our analysis suggests that in general nonconvex-nonconcave settings the models learned by simultaneous update algorithms such as gradient descent ascent are expected to generalize better than the models learned by non-simultaneous update algorithms such as gradient descent max which fully solves the maximization subproblem at every iteration. We support our theoretical results through several numerical experiments on the discussed minimax optimization algorithms.

Papers and Preprints

F. Farnia, A. Ozdaglar, “Train simultaneously, generalize better: Stability of gradient-based minimax learners”, ICML 2021

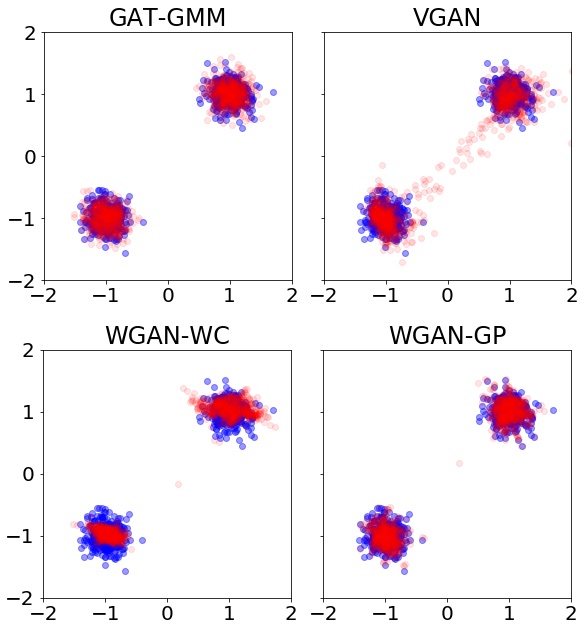Abstract: While GANs achieve state-of-the-art empirical performance in learning the complex distributions of image, sound, and text data, they perform suboptimally in learning multi-modal distribution benchmarks including Gaussian mixture models, where they are commonly outperformed by maximum likelihood-based methods such as the expectation-maximization (EM) algorithm. A natural question is whether this performance gap fundamentally exists in learning mixture distributions or is due to the poor design of the GAN players and loss function. In this research work, we design a new GAN architecture called Generative Adversarial Training for Gaussian Mixture Models (GAT-GMM) for learning mixtures of Gaussians. We prove that GAT-GMM is theoretically guaranteed to learn a mixture of two Gaussians and provide numerical results indicating that GAT-GMM can perform as well as the EM algorithm in learning Gaussian mixture models. Our results indicate that with a proper design the GAN minimax framework can potentially lead to state-of-the-art performance in learning mixture distributions.

Papers and Preprints

F. Farnia*, W. Wang*, S. Das, A. Jadbabaie, “GAT-GMM: Generative Adversarial Training for Gaussian Mixture Models”, arXiv:2006.10293

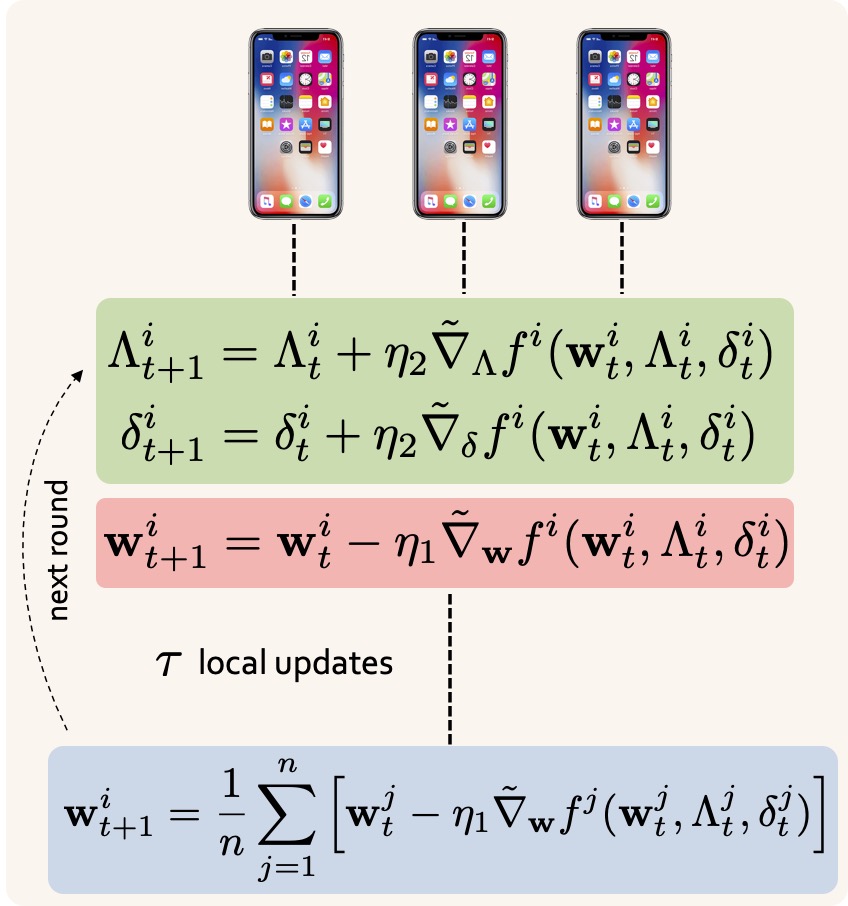Abstract: Federated learning is a recent learning paradigm where a machine learning model is trained using the training data and computational power distributed across multiple local nodes connected to a universal server node. The heterogeneity of the underlying data distributions observed by different local nodes has been an important barrier toward training robust federated learning models. In this work, we propose a minimax learning framework called FedRobust as an efficient and robust federated learning scheme against affine distribution shifts manipulating the samples observed by every node with an affine transformation. We theoretically support FedRobust by proving generalization, convergence, and distributional robustness guarantees. We perform several empirical experiments to show the robustness gain offered by FedRobust against both affine distribution shifts and unstructured adversarial perturbations.

Papers and Preprints

A. Reisizadeh*, F. Farnia*, R. Pedarsani, A. Jadbabaie, ”Robust Federated Learning: The Case of Affine Distribution Shifts”, NeurIPS 2020

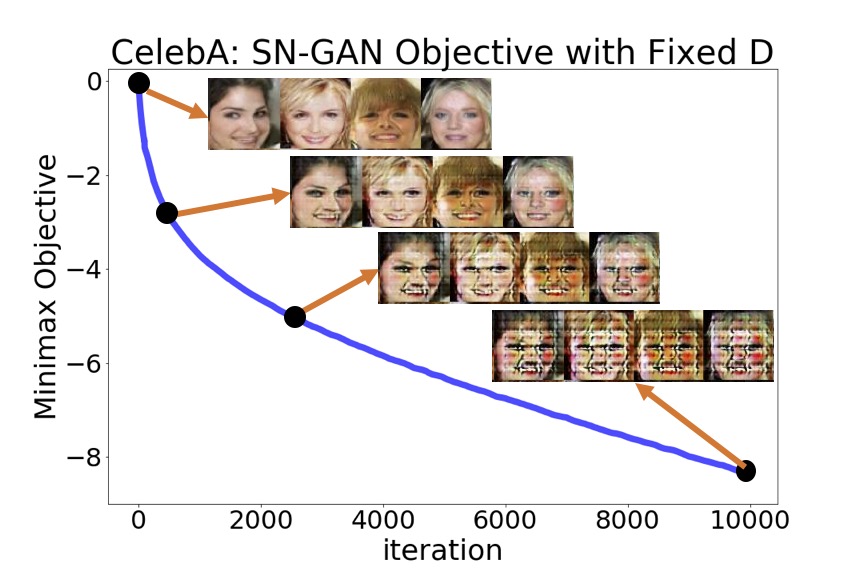Abstract: Despite the successful applications of GANs to various distribution learning problems, GAN minimax optimization remains theoretically and empirically challenging. In this work, we study the equilibrium properties of GAN problems and prove that the classical Nash equilibrium may not exist in GAN minimax games. To understand equilibrium in GANs, we propose a new notion of equilibrium, called proximal equilibrium, by considering the Nash equilibria of a different zero-sum game applying a proximal operator to the original GAN minimax objective. We prove that unlike Nash equilibria, proximal equilibria indeed exist in the minimax game of Wasserstein GANs. We then propose proximal training for GANs by optimizing the proximal objective and numerically demonstrate that proximal training can outperform standard GAN training methods.

Papers and Preprints

F. Farnia, A. Ozdaglar, “Do GANs always have Nash equilibria?”, ICML 2020

Abstract: GANs represent a minimax game between the generator and discriminator machines for learning the distribution of observed data. The GAN minimax problem with an unconstrained discriminator is known to reduce to the minimization of the Jensen-Shannon divergence between the generator’s and data distributions. However, in practice the discriminator is constrained to smaller parametrized function sets such as convolutional neural networks. In this research work, we develop a general convex duality framework for GANs and demonstrate that for a discriminator constrained to a convex set of functions, the GAN minimax problem minimizes the Jensen-Shannon divergence between two sets of probability distributions: generative models and discriminator moment matching models. We further use the proposed duality framework for interpreting and improving other minimax GAN formulations including Wasserstein GAN (WGAN) and spectrally-normalized GAN (SN-GAN) problems.

Papers and Preprints

F. Farnia, D. Tse, “A convex duality framework for GANs”, NeurIPS 2018

Abstract: Generative Adversarial Networks (GANs) have become a popular method to learn a probability model from data. In this work, we provide an understanding of basic issues surrounding GANs including their formulation, generalization and stability on a simple LQG benchmark where the generator is Linear, the discriminator is Quadratic and the data has a high-dimensional Gaussian distribution. Even in this simple benchmark, the GAN problem has not been well-understood as we observe that existing state-of-the-art GAN architectures may fail to learn a proper generative distribution owing to (1) stability issues (i.e., convergence to bad local solutions or not converging at all), (2) approximation issues (i.e., having improper global GAN optimizers caused by inappropriate GAN's loss functions), and (3) generalizability issues (i.e., requiring large number of samples for training). In this setup, we propose a GAN architecture which recovers the maximum-likelihood solution and demonstrates fast generalization. Moreover, we analyze global stability of different computational approaches for the proposed GAN and highlight their pros and cons. Finally, through experiments on MNIST and CIFAR-10 datasets, we outline extensions of our model-based approach to design GANs in more complex setups than the considered Gaussian benchmark.

Papers and Preprints

S. Feizi, F. Farnia, T. Ginart, D. Tse, “Understanding GANs in the LQG Setting: Formulation, Generalization and Stability”, IEEE Journal on Selected Areas in Information Theory, 2020

Abstract: Deep neural networks (DNNs) have set benchmarks on a wide array of supervised learning tasks. Trained DNNs, however, often lack robustness to minor adversarial perturbations to the input, which undermines their true practicality. Recent works have increased the robustness of DNNs by fitting networks using adversarially-perturbed training samples, but the improved performance can still be far below the performance seen in non-adversarial settings. A significant portion of this gap can be attributed to the decrease in generalization performance due to adversarial training. In this work, we extend the notion of margin loss to adversarial settings and bound the generalization error for DNNs trained under several well-known gradient-based attack schemes, motivating an effective regularization scheme based on spectral normalization of the DNN's weight matrices. We also provide a computationally-efficient method for normalizing the spectral norm of convolutional layers with arbitrary stride and padding schemes in deep convolutional networks. We evaluate the power of spectral normalization extensively on combinations of datasets, network architectures, and adversarial training schemes.

Papers and Preprints

F. Farnia*, J. Zhang*, D. Tse, “Generalizable Adversarial Training via Spectral Normalization”, ICLR 2019

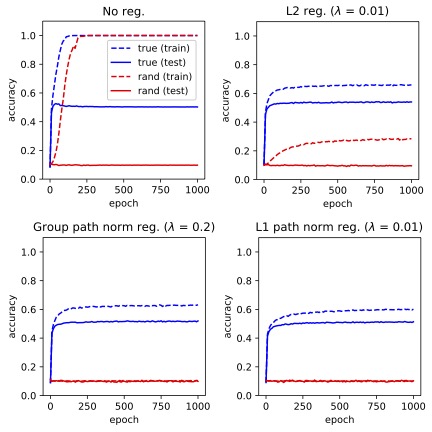Abstract: The success of deep neural networks stems from their ability to generalize well on real data; however, neural networks are observed to easily overfit randomly-generated labels. This observation highlights the following question: why do gradient methods succeed in finding generalizable solutions for neural networks while there exist solutions with poor generalization behavior? In this project, we use a Fourier-based approach to study the generalization properties of gradient-based methods over 2-layer neural networks with band-limited activation functions. Our results indicate that in such settings if the underlying distribution of data enjoys nice Fourier properties including bandlimitedness and bounded Fourier norm, then the gradient descent method can converge to local minima with nice generalization behavior. We also establish a Fourier-based generalization error bound for band-limited function spaces, applicable to 2-layer neural networks with general activation functions. This generalization bound motivates a grouped version of path norms for measuring the complexity of 2-layer neural networks with ReLU-type activation functions. We empirically demonstrate that regularization of the group path norms results in neural network solutions that can fit true labels without losing test accuracy while not overfitting random labels.

Papers and Preprints

F. Farnia, J. Zhang, D. Tse, “A Fourier-Based Approach to Generalization and Optimization in Deep Learning”, IEEE Journal on Selected Areas in Information Theory, 2020

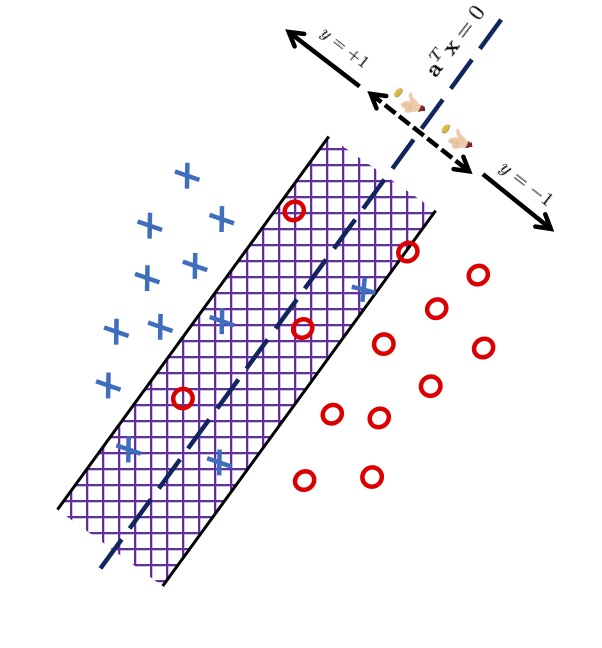Abstract: Given a task of predicting Y from X, a loss function L, and a set of probability distributions Gamma on (X,Y), what is the optimal decision rule minimizing the worst-case expected loss over Gamma? In this project, we address this question by introducing a generalization of the principle of maximum entropy. Applying this principle to sets of distributions with marginal on X constrained to be the empirical marginal from the data, we develop a general minimax approach for supervised learning problems. While for some loss functions such as squared-error and log loss, the minimax approach rederives well-known regression models, for the 0-1 loss it results in a new linear classifier which we call the maximum entropy machine. The maximum entropy machine minimizes the worst-case 0-1 loss over the structured set of distribution, and by our numerical experiments can outperform other well-known linear classifiers such as SVM. We also prove a bound on the generalization worst-case error in the minimax approach.

Papers and Preprints

F. Farnia, D. Tse, “A Minimax Approach to Supervised Learning”, NeurIPS 2016

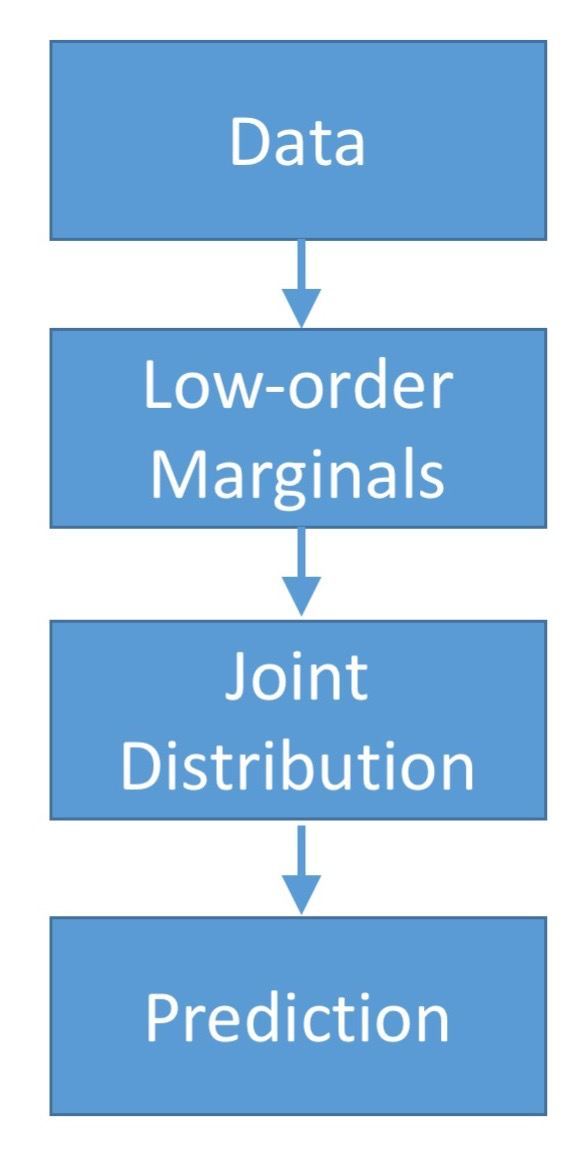Abstract: We consider the binary classification problem of predicting a target variable Y from a discrete feature vector X. When the joint probability distribution is known, the optimal classifier, leading to the minimum misclassification rate, is given by the Maximum A-posteriori Probability decision rule. However, estimating the complete joint distribution is computationally and statistically impossible for large values of d. An alternative approach is to first estimate some low order marginals and then design the classifier based on the estimated low order marginals. This approach is also helpful when the complete training data instances are not available due to privacy concerns. In this work, we consider the problem of finding the optimum classifier based on some estimated low order marginals of (X,Y). We prove that for a given set of marginals, the minimum Hirschfeld-Gebelein-Renyi (HGR) correlation principle introduced leads to a randomized classification rule which is shown to have a misclassification rate no larger than twice the misclassification rate of the optimal classifier. Then, under a separability condition, we show that the proposed algorithm is equivalent to a randomized linear regression approach. In addition, this method naturally results in a robust feature selection method selecting a subset of features having the maximum worst case HGR correlation with the target variable. We numerically compare our proposed algorithm with the DCC classifier and show that the proposed algorithm results in better misclassification rate over various datasets.

Papers and Preprints

M. Razaviyayn, F. Farnia, D. Tse, “Discrete Rényi Classifiers”, NeurIPS 2015

F. Farnia, M. Razaviyayn, S. Kannan, D. Tse, “Minimum HGR correlation principle: From marginals to joint distribution”, ISIT 2015